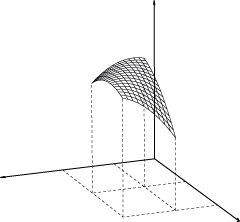
<空間座標を2次元座標になおす方法３のサンプルプログラム>

例1と同じ関数　f（x，y）　のグラフを前ページの方法で描くサンプルプログラム「　3D例1(type3).nb　」である。プログラムは最初の行（　In[1] :=　）だけしか変わっていないので,最初の行と最後のグラフだけ示す。

<3D例1(type3).nb>

In[1]:=	a1 = 0; a2 = 2; a3 = 2; c1 = 30; c2 = 75; c3 = 25; d = 3;
	b1 = a1 + (t - d)*(c1 - a1)/t;
	b2 = a2 + (t - d)*(c2 - a2)/t;
	b3 = a3 + (t - d)*(c3 - a3)/t;
	K[x_, y_, z_] := ((c1 - b1)*(c1 - a1) + (c2 - b2)*(c2 - a2) + (c3 - b3)*(c3 - a3))/
	((c1 - x)*(c1 - a1) + (c2 - y)*(c2 - a2) + (c3 - z)*(c3 - a3));
	q1[x_, y_, z_] := c1 + K[x, y, z]*(x - c1);
	q2[x_, y_, z_] := c2 + K[x, y, z]*(y - c2);
	q3[x_, y_, z_] := c3 + K[x, y, z]*(z - c3);
	i1 = (b1 - a1)/(t - d); i2 = (b2 - a2)/(t - d); i3 = (b3 - a3)/(t - d);
	tt2 = (b1 - a1)^2 + (b2 - a2)^2; tt3 = (b3 - a3)^2 + tt2;
	j1 = k2*i3 - k3*i2; j2 = k3*i1 - k1*i3; j3 = k1*i2 - k2*i1;
	FX[x_, y_, z_] := (q1[x, y, z] - b1)*j1 + (q2[x, y, z] - b2)*j2 + (q3[x, y, z] - b3)*j3;
	xma = 3; yma = 4; zma = 3; yahaba = 1.9;
	xxd = Abs[FX[0, yma,0] - FX[xma, 0, 0]];
	yyd = Abs[FY[0, 0, zma] - Min[FY[xma, 0, 0], FY[0, yma, 0]]];
	ar = yyd/xxd; wx = (t/d)*xxd/50; hx = yahaba*0.2*wx;
	wz = (t/d)*yyd/50; hz = yahaba*wz*0.2; wy = wx; hy = hz;
	LX = {Thickness[0.00402], {
	Line[{{FX[0, 0, 0], FY[0,0, 0]}, {FX[xma, 0, 0], FY[xma, 0, 0]}}]},
	{Line[{{FX[xma - wx, hx, 0],
	FY[xma - wx, hx, 0]}, {FX[xma, 0, 0], FY[xma, 0, 0]},
	{FX[xma - wx, -hx, 0], FY[xma - wx, -hx, 0]}}]}};
	LY = {Thickness[0.00402], {
	Line[{{FX[0, 0, 0], FY[0,0, 0]}, {FX[0, yma, 0], FY[0, yma, 0]}}]},
	{Line[{{FX[0, yma - wy, hy], FY[0, yma - wy, hy]},
	{FX[0, yma, 0], FY[0, yma, 0]},
	{FX[0, yma - wy, -hy], FY[0, yma - wy, -hy]}}]}};
	LZ = {Thickness[0.00402], {
	Line[{{FX[0, 0, 0], FY[0,0, 0]}, {FX[0, 0, zma], FY[0, 0, zma]}}]},
	{Line[{{FX[0, hz, zma - wz],
	FY[0, hz, zma - wz]}, {FX[0, 0, zma], FY[0, 0, zma]},
	{FX[0, -hz, zma - wz], FY[0, -hz, zma - wz]}}]}};
Out[13]:=	- Graphics -