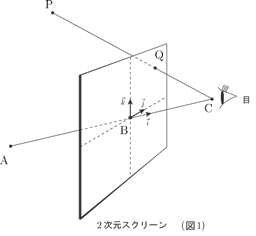
目の位置が C ( c₁ ，c₂ ，c₃ ） で，点 A （ a₁ ，a₂ ，a₃ ） に焦点を合わせている．点C　からの距離が d である 2次元スクリーンと線分 AC の交点を B とする．

　 BC = d である． AC = t とすると点 B の位置ベクトルは

OB	=	OA	+	t-d	AC
				t

である．今，空間の任意の点P （ x , y , z ） に対し，線分 PC と 2 次元スクリーンの交点を Q （ q₁ ， q₂ ， q₃ ） とおく．

CQ

=

K

CP

とすると定数K　は

K =	CB ・ AC   CP ・ AC

で求まる．ただし

CB ・ AC

は

CB

と

AC

の内積である．よって点Qの位置ベクトルは

=　 　+　K　 OQ OC CP

で求まる．今

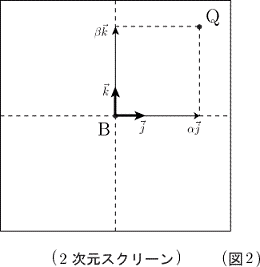
とおくと　は正規直交基底（図1）である．点Bを2次元スクリーン（図2）上の原点と考える．点 Q のこのスクリーンにおける相対座標 （ α ，β）は

より，α　=	BQ	・	j	，	β　=	BQ	・	k	（内積）

で求まるから，点 Q の相対的な平面座標 （FX ， FY ） は

FX = α =	BQ	・	j	，　FY　=　β　=	BQ	・	k	で求まる．