微分積分学講義

微分積分学講義培風館（1996）

まえがき

　本書は、将来数学を使う立場に立つ学生諸君を対象として、微分積分学を分かり易く興味を持って学習できることを願って書かれた教科書である。微分積分学は線形代数学とならんで数学の中でも最も基礎的な概念と計算方法を与えるものであり、理工系のみならず経済学などの社会科学の分野においても、数学的な解析を進める上でなくてはならない教科である。

　本書では、高等学校の『数学１、２』の範囲を予備知識として理解でき、その延長として微分積分学を円滑に学ぶことが出来るように配慮し、また数学を応用する立場から、定理の厳密な証明よりもむしろ定理を性格に適用し、計算することに重点をおいている。

　内容については、通常の微分積分学の項目のほかに、とくに応用上重要とおもわれる数値積分、ニュートン法およびフーリエ級数展開についてに基礎的な事柄を説明した。各章には、「例題と研究」という節を設け、本文中で省略したていりの証明,約に立つと思われる公式や例題を解説した。コンピュータは年々使いやすくなり、複雑な計算もいとも簡単に答えをだしてくれるようになったが、各章末に上げた練習問題では、筆算で計算することにより、理論や計算原理を理解し、計算力を養う上で役立つことを願っている。しかし本書では、計算が必ずしも得意でない学生諸君のために、例題や練習問題の解答は自明でないかぎり丁寧に解説した。

　以下各章ごとに内容の概略を述べる。

１．数と初等関数

　第１章では、実数上で定義される関数の概念を説明し、いわゆる初等関数：有理関数、指数関数と対数関数、三角関数と逆三角関数などの定義と基本的な性質を述べる。

２．関数の極限と連続性

　極限は微分積分学にとって最も基本的な操作である。関数の連続性や微分可能性は極限によって定義される。また次の公式は三角関数や指数関数の導関数の計算に不可欠である。

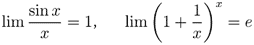
　また、合成関数の定義及び有界閉区間での連続関数の性質も述べる。

３．微分係数と導関数

　第３章では微分係数、導関数の定義を与えたのち微分法の公式、合成関数と逆関数の導関数の計算公式を述べ、ついで指数関数と対数関数、三角関数と逆三角関数などの導関数を与える。また、ライプニッツの公式など高階導関数の計算についても述べる。

４．平均値の定理とテーラー展開

　微分学の中で最も重要な部分である、平均値の定理、テーラーの定理を証明する。これをもとにして、無限回微分可能な関数がテーラー展開可能であるための１つの十分条件を与える。テーラーの定理は関数を多項式で近似することであり、またテーラー展開は関数を整級数に展開することである。さらに微分法の応用として関数の増減と極値問題を取り扱う。

５．偏微分とその応用

　自然界の現象や、工学上または経済学上などの問題を解析しようとするとき、独立変数が１つだけの数学では適用が限られてしまう。そこで、第５章では独立変数がいくつかある場合の微分法について述べる。２変数関数を中心に取り扱うが、そのほとんどは、そのまま３変数以上の関数に対して拡張できる。偏微分と偏導関数、高階偏導関数、合成関数の偏導関数、２変数関数の平均値の定理とテーラー展開などについて述べたのち、応用として極値問題を取り扱う。例題と研究の項で条件付き極値問題を取り上げる。

６．不定積分

　本章ではびぶんお逆演算である不定積分とその計算方法について述べる。第７章において図形の面積としての定積分を解説するが、定積分は１つの数であるのに対して、不定積分は関数の族を表している。この２つの概念を結び付けているのが微分積分学の基本定理であって不定積分が求まれば定積分も計算できることになる。不定積分を求めることは１階常微分方程式を解くときにも利用される。

７．定積分

　定積分はリーマン和の極限として定義される。定積分の基本的な性質を述べたのち微分積分学の基本定理を証明する。これにより

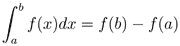
が成り立つ。ここでF(x) はf(x) の不定積分である。ついで広義積分を定義する。定積分の応用として曲線の長さ、およびフーリエ級数展開について解説する。

８．重積分

　定積分は２変数や３変数などの多変数関数に対しても定義できてこれらを重積分という。２重積分もリーマン和の極限として定義されるが、その幾何学的意味は体積と思ってよいであろう。重積分の計算は、実際には１変数の積分を繰り返して計算する方法、即ち累次積分が用いられる。１変数関数の積分では変数変換が有効に用いられたが、重積分においても積分変数の変換公式が重要である。特に極座標変換はしばしば利用される。

９．数列と級数

　本章では数列と級数の基礎的な事柄について述べる。第２章でのべたように数列の極限は微分積分学において基本的な役割を果たしている。それだけでなく応用上も大切で例えば非線形方程式の根はニュートン法と呼ばれる数値計算によって、１つの数列の極限として得られることを述べる。また、級数については正項級数の収束判定条件、及びべき級数の収束半径などが主な内容である。１つの応用として超幾何級数の収束、発散について述べるがこれは例えば水素原子の波動関数を決定するときに基礎的な役割を果たしているのである。

１０．常微分方程式

　自然現象や理工学上の問題、あるいは現実社会の問題を理解するために我々は単純化したり適当な仮定をしたりして、実際の問題を数学の問題に書き換える操作を行う。このようにして構成された数学上の問題が、現実の問題の数学モデルというわけである。数学モデルを解くことによって、実際の問題に対して、説明、予測、決定、そして計画に役立てることが出来る。多くの問題が常微分方程式で表される数学モデルに帰着される。そこで第10 章では、与えられた常微分方程式の解を求めるいくつかの方法を述べる。１階常微分方程式、２階常数係数線形微分方程式の解法が主な内容である。例題と研究の項で力学的振動系と電気回路を取り上げる。